编译原理-数据流分析-冗余消除

本章博客将介绍一种消除程序代码冗余的编译器代码优化技术 --- 懒惰代码移动算法

什么是冗余消除

冗余消除就是要尽量减少表达式求值的次数，避免形如\(x+y\)的表达式在之后的代码中多次计算，影响性能。

冗余的来源主要有以下三种：

若对于含有表达式如 \(a+b\) 的基本块 \(B\)，任意到 \(B\) 的路径都已经对 \(a + b\) 求过值，则我们称这个表达式在 \(B\) 中冗余，是公共的子表达式。这样的表达式就不需要在 \(B\) 中重新计算。

注意，此时在 \(a+b\) 被计算后，表达式中的分量 \(a,b\) 不能在 \(B\) 之前被重新定值，否则这样的表达式不是一个可用表达式。

对于类似 \((a + b) ^ c + d\) 这样的更深层的子表达式，我们可以重复利用公共表达式消除技术直至没有新的公共表达式来找到这样的深层子表达式，当然我们也可以参考常量传播框架来实现类似的搜索，当然也可以参考LLVM的模式匹配来达到同样的效果。

假设 \(a\)，\(b\) 没有在循环 \(L\) 中重新定值，那么 \(a+b\) 就是对于 \(L\) 循环不变的，这样的循环不变式可以提出循环，减少不必要的计算。以下是一个循环不变式的例子：

1
2
3

while (c){
    print(a + b)
}

可以转化为：

t = a + b
while (c){
    print(t)
}

为了保证 while 循环中循环不变表达式可以被优化，编译器通常把：

1
2
3

while c {
    S;
}

表示为：

if c {
    repeat
        S;
    until not c
}

这样循环不变式可以放在 repeat-util 之前。

对于以下基本块结构：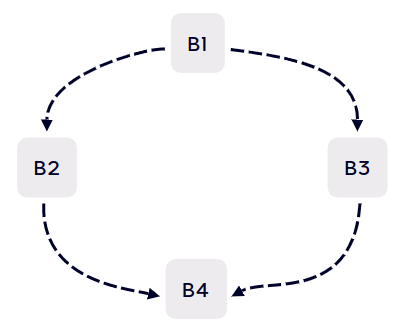

若 \(B_2\) 中计算了 \(a+b\) ，但 \(B_3\) 中没有计算 \(a+b\)，\(B_4\) 中计算了 \(a+b\)，那么

可以说在 \(B_1 \rightarrow B_2 \rightarrow B_4\) 上 \(a+b\) 冗余，在\(B_1 \rightarrow B_3 \rightarrow B_4\)上 \(a+b\) 不冗余，那么该表达式对 \(B_4\) 就是部分冗余的

对于这样部分冗余的表达式，我们需要在 \(B_3\) 与 \(B_4\) 之间插入新的基本块来计算 \(a+b\) 。

为了解决部分冗余的问题，我们设计了懒惰代码移动算法，它有以下性质：

逆向数据流分析找到各个程序点上的 预期执行(anticipated) 的表达式。 > 预期执行(anticipated) 指的是：从程序点 \(p\) 出发的所有路径都会计算 \(a+b\) 的值，且 \(b,c\) 的值就是他们在 \(p\) 上的值 > > 预期执行决定了一个表达式可以放的有多靠前，而一个表达式越靠前，能消除的冗余就越多
将对表达式的计算放在满足下面条件的程序点上：总存在路径使得该点是此路径第一个预期执行该表达式的点。同时我们称程序点可用(available)当所有到达该程序点的原有路径中该表达式都被预期执行，这个过程可以通过前向数据流分析完成。
后延表达式，一个表达式可被后延到某个程序点的条件为：到该点的所有路径上，该表达式已经在程序点前预期执行，但没有使用该表达式。该过程可以通过前向数据流分析完成。
最后使用简单的逆向数据流分析删除那些给程序中只使用一次的临时变量赋值语句。

方向：逆向

传递函数：\(f_B(x)=use_B \cup (x-kill_B)\)

交汇运算：\(\cap\)

方向：正向

传递函数：\(f_B(x)=(anticipated[B].in \cup x) - kill_B\)

交汇运算：\(\cap\)

方向：正向

注意，这里定义\(earliest[B]=anticipated[B].in - available[B].in\)

传递函数：\(f_B(x)=(earliest[B] \cup x) - kill_B\)

交汇运算：\(\cap\)

方向：逆向

注意，这里定义 \[ latest[B]=(earliest[B] \cup postponable[B].in) \cap (use_B \cup \neg(\bigcap_{S,succ(B)}{earliest[S]\cup postponable[S].in})) \]

传递函数：\(f_B(x)=(use_B \cup x) - latest[B]\)

交汇运算：\(\cup\)