SAT-布尔可满足性理论

什么是约束求解？

现实世界中有许多问题可以被抽象为基于约束(Constraint)的问题，约束指的是就是条件。
而约束求解就是在给定约束的情况下，如果可满足(Satisfiable)我们就返回一组解，如果不可满足，我们就给出一个较小的矛盾集(Unsatisfiable core)。

约束求解是不可判定(Undecidable)的问题，但许多子问题是可判定的。比如求解一个不等式组 \(a < 0 \&\& b > 0\) ，我们有一组可满足的解 \(a = -1, b = 1\)，但对于\(a < 0 \&\& a > 0\)，我们不可能满足该命题，故我们需要给出矛盾集 \(\{1, 2\}\)。其中\(1\)指的就是第一个命题\(a < 0\)成立，\(\{1, 2\}\) 则是两个命题同时成立，显然，这个命题集合是矛盾的。

SAT-布尔可满足性问题就是一种约束求解问题，该问题是 NP-complete 的，除此之外线性方程组、不等式组之类的求解问题同样属于约束求解问题。

Notations

文字(literal): 布尔变量 \(x\)
子句(clause): 文字的析取(disjunction): \(x \vee \neg y\)

那么 SAT 就是给定一组子句，寻找对各文字(或者布尔变量)的赋值使得所有子句为真。

其实就是使子句的合取为真: \((\neg x \vee y) \wedge x\)

穷举法

最简单的暴力解法，一个个试就行了， \(O(2^n)\)的复杂度，过于慢了。

DPLL

冲突(Conflict)检测

对于一个赋值\(\{x, y\}\)，我们可以推出 \(x \vee y\) 与 \(x \vee \neg y\)是冲突的，即两个子句在该赋值下无法同时为真，那么我们不需要完整赋值就可以排除该情况。这时我们有伪代码：

Sat(assign) {
  if (conflict(assign)) return false;
  if (complete(assign)) return true;
  choose a unassigned x；
  return sat(assign ∪ {x=0}) || sat(assign ∪ {x=1})
}

标准推导方法

Unit Propagation: 其他文字都为假，剩下的一个文字必定为真
Unate Propagation: 当一个子句存在为真的文字时，可以从子句集合中删除
Pure literal elimination: 当一个变量只有为真或者为假的形式的时候，可以把包含该变量的子句删除

最后我们根据以上两个方法得到算法：

dpll(assign) {
  assign’ = assign_prop(assign);
  if (conflict(assign’)) return false;
  if (complete(assign’)) return true;
  choose a unassigned x；
  return dpll(assign’ ∪ {x=0}) || dpll(assign’ ∪ {x=1});
}

其中 assign_prop 是推导方法，

这里还有一些预处理/归结/Resolution 方法如：

Probing: 如果 x=0 或者 x=1 都能推导出 y=0，则推导出 y=0
Equivalence: classes
预先检查出等价的子句集合，然后删除其中一个
{1, 2, -3}
{2, 1, -3}

早期存在完全基于归结，不穷举赋值的算法（DP 算法），但速度通常显著落后于 DPLL

变量选择有很多的 heuristics，有基于子句集，也有基于历史的，这里就不多写了。

CDCL -- Conflict-Driven Clause Learning

核心思想很简单：遇到 conflict 的时候，把和 conflict 相关的布尔赋值取反加入子句集，若\(x \wedge y \wedge z\)导致了冲突，那么我们加入子句\(\neg x \vee \neg y \vee \neg z \vee\)，通过这种方式，我们不再需要记录之前遍历过的赋值，每次任意选择剩下的变量和赋值即可，因为从新添加约束出发的推导实际保证了之前探过的冲突赋值不会出现。

这里有个新问题，寻找什么样的切割，让决策节点和矛盾不联通？参考北大 PPT: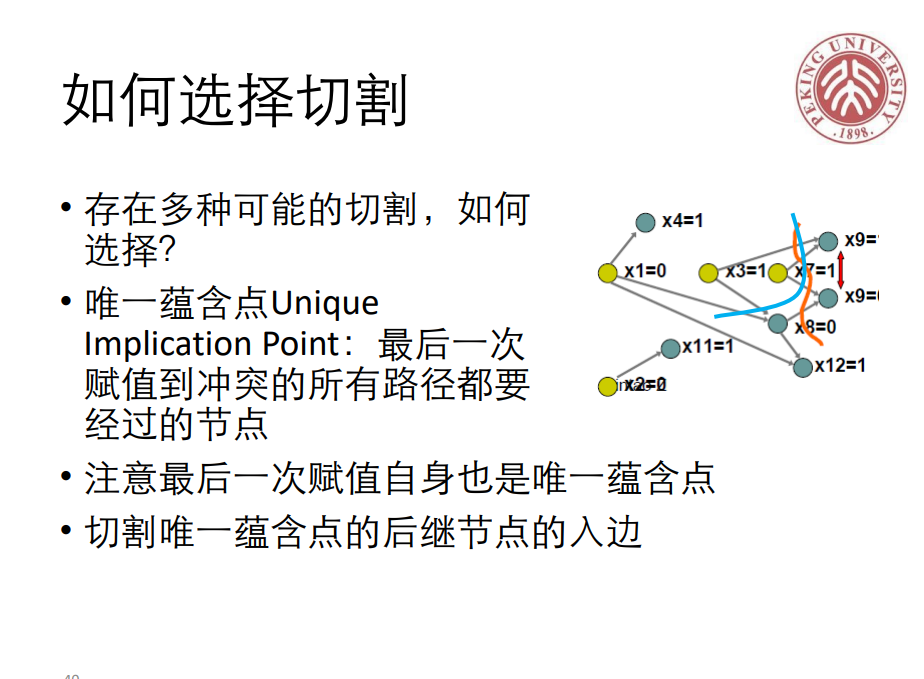

这里也有个可互动的例子来解释这个算法：Conflict Driven Clause Learning

同样，这里也有个英文的解释：

Non-Chronological Backtracking
When CDCL learns a clause, it backtracks to the clause’s asserting level.
You can just think of this meaning that it backtracks to the latest guess that affects a literal in the learned clause. Since this clause has x1 and x5, and x1 was the latest one to be guessed in that clause, we backtrack to when we set x1 to be True. When we backtrack to this level, the learned clause will immediately be available for BCP letting us put into action what we just learned!

最后，我们有伪代码：

dpll(assign) {
assign = {};
  while(true) {
  assign’ = assign_prop(assign);
  if (conflict(assign’)) {
    if(assign is empty) return false;
    add new constraint;
    backtrack;
  } else {
    if (complete(assign’)) return true;
    choose a unassigned x；
    assign = assign'
    add x into assign
  }
}

这个方法使后来的 SAT/SMT 速度变得特别快

Reference

北大软件分析 Conflict Driven Clause Learning