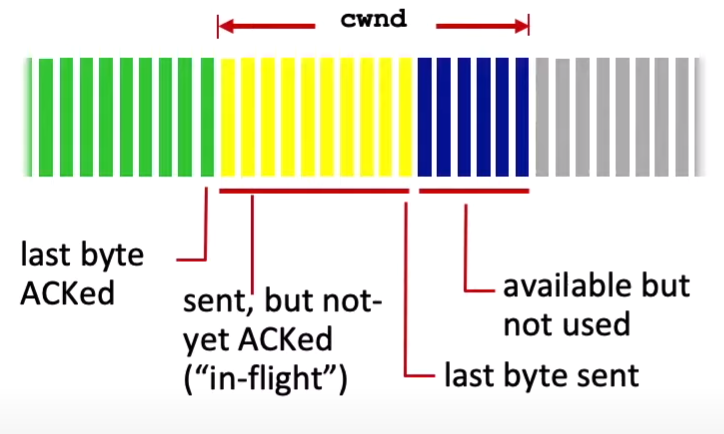
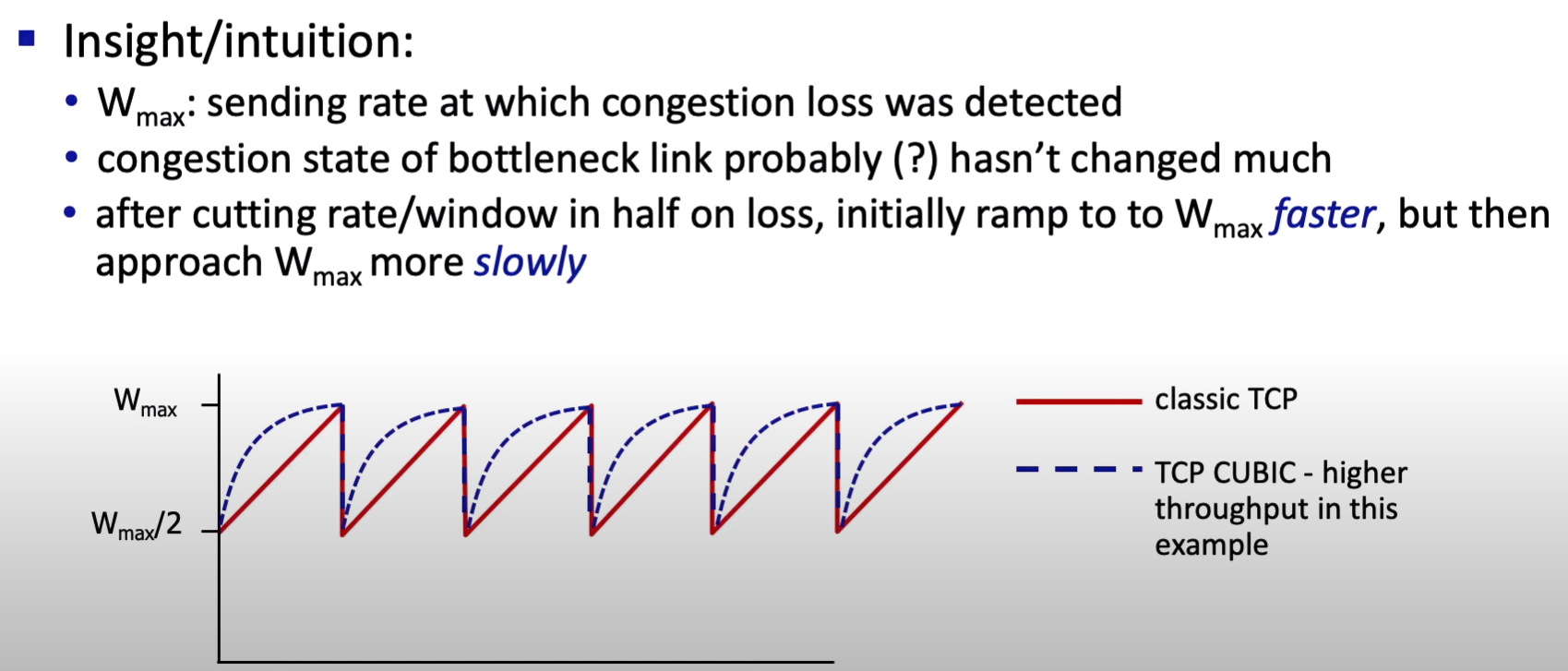
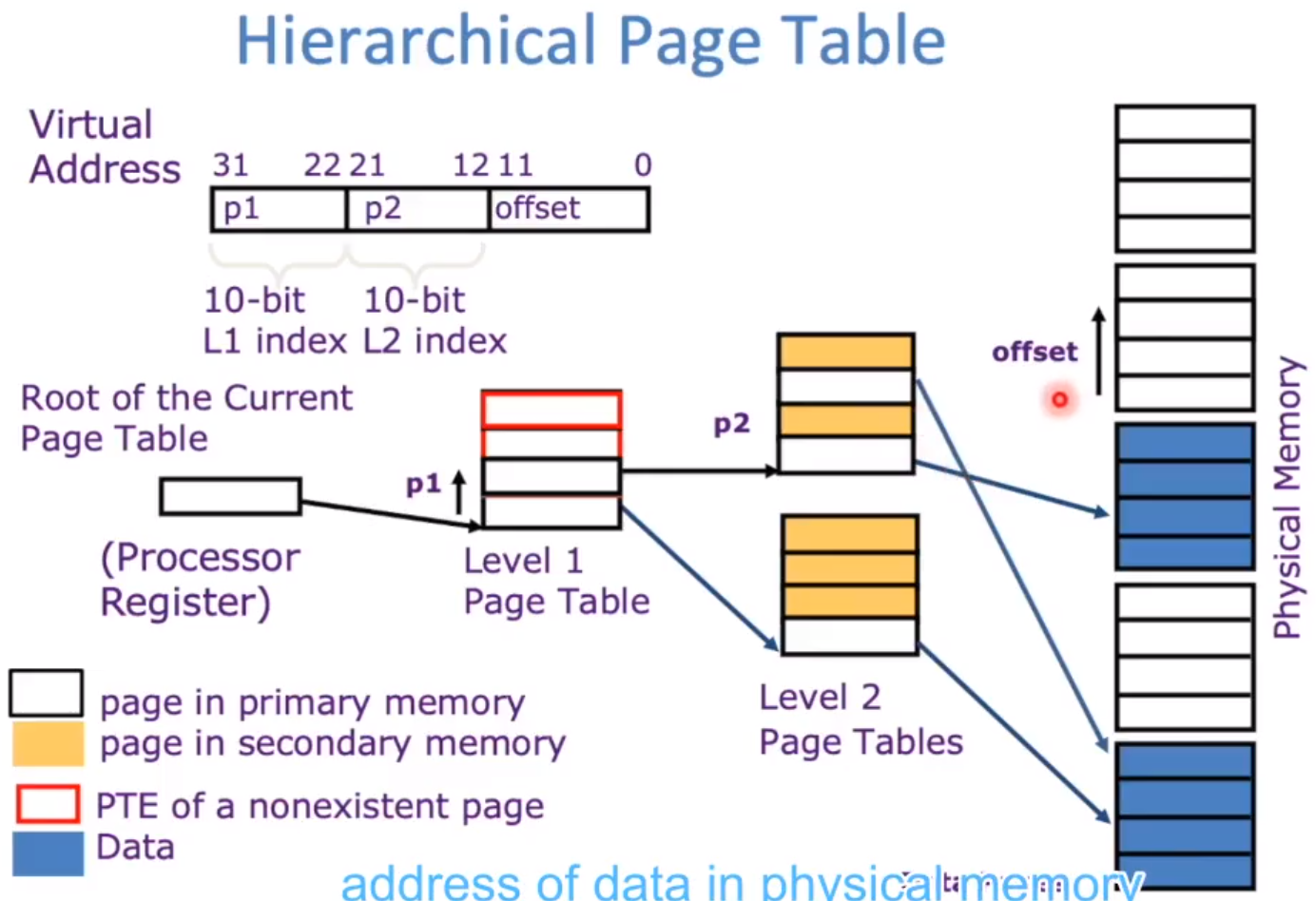
题目描述: 
动态规划
简单想法:
使用动态规划,令 \(dp[i][j]\) 为 是否 \(s[0..i]\) 与 \(p[0..j]\) 匹配 ,也就是 s 前 i 个字符与 p 前 j 个字符匹配。
则有初始状态:
\[dp[0][0] = true\]
由于长度大于 0 的字符串不可能被长度为 0 的模式匹配,故令:
\[dp[i][0] = false, 0 < i \le sn\]
同时长度为 0 的字符串只可能被形如"*"这样全为通配符的模式匹配,故令:
\[dp[0][j] = dp[0][j-1] \quad \wedge \quad p[j-1] = '*'\]
状态转移方程则为:
\[ \begin{equation*} %加*表示不对公式编号 \begin{split} dp[i][j] = & dp[i][j - 1] \wedge p[j - 1] = '*' \quad \vee \\ & dp[i - 1][j] \wedge p[j - 1] = '*' \quad \vee \\ & dp[i - 1][j - 1] \wedge (s[i - 1] = p[j - 1] \vee p[j - 1] = '?' \vee p[j - 1] = '*') \end{split} \end{equation*} \]
故我们可以有代码:
1 | bool dp[2001][2001]; |
时间复杂度为 \(O(mn)\), 空间复杂度为 \(O(mn)\)
贪心(LeetCode 题解)
前一方法的瓶颈在于对星号 \(*\) 的处理方式:使用动态规划枚举所有的情况。由于星号是「万能」的匹配字符,连续的多个星号和单个星号实际上是等价的,那么不连续的多个星号呢?
我们以 \(p=∗ abcd ∗\) 为例,ppp 可以匹配所有包含子串 abcd 的字符串,也就是说,我们只需要暴力地枚举字符串 s 中的每个位置作为起始位置,并判断对应的子串是否为 abcd 即可。这种暴力方法的时间复杂度为 O(mn),与动态规划一致,但不需要额外的空间。
如果 p=∗abcd∗efgh∗i∗ 呢?显然,ppp 可以匹配所有依次出现子串 abcd、efgh、i 的字符串。此时,对于任意一个字符串 sss,我们首先暴力找到最早出现的 abcd,随后从下一个位置开始暴力找到最早出现的 efgh,最后找出 i,就可以判断 sss 是否可以与 ppp 匹配。这样「贪心地」找到最早出现的子串是比较直观的,因为如果 sss 中多次出现了某个子串,那么我们选择最早出现的位置,可以使得后续子串能被找到的机会更大。
因此,如果模式 ppp 的形式为 \[* u_1 * u_2 * u_3 * \cdots * u_x ∗\] ,即字符串(可以为空)和星号交替出现,并且首尾字符均为星号,那么我们就可以设计出下面这个基于贪心的暴力匹配算法。算法的本质是:如果在字符串 sss 中首先找到 \(u_1\) ,再找到 \(u_2, u_3, \cdots, u_x\),那么 s 就可以与模式 p 匹配,伪代码如下:
1 | // 我们用 sIndex 和 pIndex 表示当前遍历到 s 和 p 的位置 |
当然还有一些特殊情况,如星号不总是出现在前后,此处省略。 时间复杂度: 渐进:\(O(mn)\),平均复杂度:\(O(m\log{n})\) 具体的分析可以参考论文On the Average-case Complexity of Pattern Matching with Wildcards,注意论文中的分析是对于每一个\(u_i\) 而言的,即模式中只包含小写字母和问号,本题相当于多个连续模式的情况。由于超出了面试难度。这里不再赘述。
空间复杂度:O(1)
此外(LeetCode 官方题解)
在贪心方法中,对于每一个被星号分隔的、只包含小写字符和问号的子模式 \(u_i\) ,我们在原串中使用的是暴力匹配的方法。然而这里是可以继续进行优化的,即使用 AC 自动机 代替暴力方法进行匹配。 由于 AC 自动机本身已经是竞赛难度的知识点,而本题还需要在 AC 自动机中额外存储一些内容才能完成匹配,因此这种做法远远超过了面试难度。 这里只给出参考讲义 Set Matching and Aho-Corasick Algorithm:
讲义的前 6 页介绍了字典树 Trie;
讲义的 7−19 页介绍了 AC 自动机,它是以字典树为基础的;
讲义的 20−23 页介绍了基于 AC 自动机的一种 wildcard matching 算法,其中的 wildcard \(\phi\) 就是本题中的问号。
感兴趣的读者可以尝试进行学习。